Intervals in depth

Learn here about the semitone, the octave, and how Western music singles out 12 pitches per octave, whose sounds are 0 to 11 semitones above that of whichever pitch is measured from.?? The instrument determines how to produce these pitches, often with more than one possibility with stringed instruments.?? Interval shapes for guitar (bass, piano) are presented.?? The really common intervals are covered later in these beginner lessons, where you’ll see that the intervals of 3 or 4 semitones are present in many scales, and divide these scales into two families: major-based and minor-based.
Intervals – Introduction
The interval shapes below are interactive, if you’re reading this inside emuso.?? Click on a shape to see and hear it on “guitar”, where you drag it around by the anchor (solid red circle) to better understand what happens as the shape moves across strings.
If you prefer watching a video, this video covers the basics, with some musical examples.?? But it doesn’t cover every interval shape, which are available below.
An interval is the sound made by two pitches some number of semitones apart.
Intervals are incredibly useful, as sounds for creating different levels of tension in your audience, melodically and harmonically. Intervals are present in every scale and chord shape, making it simple to remember these, and know which notes in those shapes need more emphasis.
This article starts with the concept of the semitone and the octave, physical properties of sound, and fundamental to musical intervals.
This is followed by how the guitar is tuned, for standard tuning. Then we look at the interval sizes (in semitones) created between different strings at the same fret, which I call the ???vertical interval??? as its shape runs parallel to a fret, vertical to the guitar neck. Then we look at intervals starting with their possible shapes on a guitar in standard tuning, to create the fundamental twelve intervals of Western music within an octave. Their theory-based names are given, along with their semitone equivalents. There are a few additional one???s theory recognises, which are found an octave above. The octave shape for guitar is then given. If you want to improve how you navigate the fretboard, this is vital information. Next we categorise the intervals roughly into four groups, based on how stable or clashy their sounds are, hence what is expected to follow. This is independent of instrument type.
This is followed by a brief look at the physical aspects of vibrating strings (frequency, and overtones) that make up the sounds produced by musical instruments, resulting from the way an instrument is constructed). Lastly, the concepts of pitch and timbre are briefly looked at ??? these are how our brains perceive vibrating air molecules arriving at our ears.
Interval names
We tend to use interval symbols (e.g. b3) , or semitones, across the emuso blog, and in interactive lessons for emuso/Studio, and in the user interface for emuso/PracticeSuite PRO.?? This means less jargon to deal with.???? We also typically look at intervals within an octave from the nearest, lowest chord root, or from the nearest, lowest tonic.?? This is much easier for visualisation and improvisation.?? This means that, other than in chord names, we don’t show 9ths and 11ths and 13ths … rather we’ll show 2, 4, and 6 in the relevant octave.
However, standard music theory does single out the occurrence of 2nds, 4ths and 6ths in higher octaves from the lowest?? chord root, or tonic, and refers to these as 9ths and 11ths and 13ths.?? Though it is inconsistent what the yardstick pitch is being chosen to measure from.?? For example, in a piano voicing of a sus2 chord, the right hand may play 1, 2, 5, with the left hand playing the 1 in the bass, one or more octaves lower.?? But standard theory doesn’t call the 2 a s a 9 in this situation.?? Whereas in 4-part writing, over a couple of octaves, with the 2 in the upper octave, it is referred to as a 9.
See here for all the interval names used in music theory.?? They are helpful, potentially, in discussions with other musicians, although symbols like “b3” or “#4” are widely known.
Semitone and octave
A tuning system, known as the 12-tone equal temperament, introduced the idea of singling out 12 specific frequencies within an octave. For example, the frequency 440Hz (also called A440, and A4) is used to tune the sound of the 5th fret on the treble E string of a 6-string guitar.
An octave higher is the frequency 880 Hz, created at the 17th fret (5 + 12), and the other frets (6, 7, 8, ??? 14, 15, 16) create sounds of these other specific frequencies in the octave starting at A440. Each of these frequencies are said to be a semitone apart. Thus, in the octave we have specific sounds chosen that are 0 to 11 semitones higher than the sound used for the start of the octave (such as 440Hz). Starting at 880 Hz, we again divide the octave from here to 1760 Hz into 12 semitones. For example, the sound whose frequency is 3 semitones above 880 Hz, is an octave above the sound whose frequency is 3 semitones above 440 Hz. Each of these specific frequencies in the octave starting at 880 Hz is an octave above its equivalent in the octave starting at 440 Hz.
These frequencies are mathematically determined. Two frequencies are a semitone apart if f2 = f1 x 1.059 (roughly). See https://newt.phys.unsw.edu.au/jw/notes.html for details. So, if multiply 440 by 1.059, we get the frequency of sound one semitone higher. Multiply that sound by 1.059, and this sound is one semitone higher than its predecessor, and two semitones higher that 440 Hz. If we keep doing, by the time we get to 12th frequency (12 semitones), we get the octave (880 Hz). Note names are assigned to each of these frequencies.
Tuning
In standard tuning, the open strings are (lazily) referred to, from bass string to treble string, as E, A, D, G, B, E. These are named E2, A2, D3, G3, B3, E4. The number indicates the octave.
In standard tuning, the note at the 5th or 4th fret is tuned to match the adjacent open string note. Below, the same colour notes are identical in pitch…
As a result, the pair of notes at any same fret on any of the string pairs (E,A), (A,D), (D,G) and (B,E) make an interval of 5 semitones. I call this the ???vertical interval??? at any same fret between adjacent strings. On the remaining string pair (G,B), the vertical interval is 4 semitones.
Interval shapes
Shapes that involve two adjacent strings may include “(G,B)” in their title. “(G,B)” means this shape only applies on the G,B pair of strings. If “(G,B)” is omitted, the shape is the same on all other adjacent string pairs, other than the G,B pair.
b2 (minor 2nd, 1 semitone) and 2 (a major 2nd, a tone, two semitones) … useful for continuing scale pattern across adjacent strings, as in most scales, like major and its modes, all neighbouring notes are a b2 or a 2 apart.
b3 (minor 3rd, 3 semitones) and 3 (major 3rd, 4 semitones) are responsible for dividing our music into minor and major.
1

1 (G,B)

b2

b2 (G,B)

2

2 (G.B)

b3

b3 (G,B)

3

3 (G,B)

4

4 (G,B)

#4, b5

#4, b5 (G,B)

5

5 (G,B)

5

5

5

5

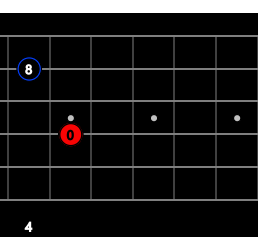
#5, b6

#5, b6 (G,B)

#5, b6

#5, b6

#5, b6
#5, b6

6

6

6

6

b7

b7

b7

b7

7

7

7

7

octave

octave

octave

octave

octave

octave

octave

The 12-fret octave shape

Intervals stability
The expectation created by an interval depends on whether the music (ignoring modes) is based on the major scale or one of the main minor scales (natural minor, harmonic minor, or melodic minor).
For a full treatment for the major scale, see here.
For an introduction to the various minor scales in the Western minor system, and full treatment of the stability of the intervals in natural minor (aeolian), see here.
A post for the handling of the upper tones in harmonic minor and melodic minor is coming 14 Aug 2021.
Ninths, elevenths and thirteenths
(b,#)9 is the same as (b,#)2, an octave higher.?? Chords with a (b,#)9 in the name are often voiced with a (b,#)2. (b)13 is same as (b)6, an octave higher.?? Chords with a (b)13 in the name are often voiced with a (b)6. (#)11 is same as (#)4, an octave higher.
When improvising, it is convenient just to think of intervals from the unison to the maj7, relative to the nearest lower chord root or scale tonic note (remember, all octaves of the root or tonic have the same note name, and are equally usable
Vibrating strings
When a string is bowed or plucked (or hit, with a piano), the string vibrates.?? The length of the string that is vibrating, along with its tension, and its mass (thickness), and what is made from, determines how fast the string vibrates (the frequency of vibration, known as the fundamental frequency).
On fretted and fretless stringed instruments, like guitar and violin, the length of the string vibrating is from the point where it is held down, to the next point of contact, the bridge.
On piano, pressing a piano key causes a hammer to hit one or more identical strings ??? most of the piano keys are each associated with their own identical three strings (for a richer sound).?? The strings are various lengths (the bass sounding strings being the longest).?? The bass piano keys use two strings.?? The very treble piano keys use one string.
Multiples of the fundamental frequency, called harmonics, are also introduced, for example, 1x, 2x, 3x, 4x of the fundamental frequency (and so on).?? The strengths (amplitudes) of these different frequencies fluctuate over the time the sound lasts for.?? These are very much influenced by how the instrument is constructed, and the materials used, as the vibrations go through the instrument body as well.
The strengths are also affected by how hard the piano key is pressed, or how hard a string is plucked or bowed.?? On guitar, we can cut out some of these overtones if we lightly touch or tap the vibrating string with a finger of our picking hand (touched harmonic, tapped harmonic), or by picking the string with a particular technique (pinched harmonic).?? Vibrato and bends affect these frequencies as well.
On piano, releasing the piano key applies a damper to its associated string(s) stopping them vibrating.?? On guitar, say, eventually the plucked string dies out, until plucked again.?? On violin, this is when the bowing stops.
PITCH, TIMBRE
If we listen to a pure sound, with only one frequency (such as a pitchfork, or a sine wave produced by a synthesiser), our brains perception of this is called a pitch.
Usually, we are listening to the sound of a piano key or a fretted guitar string ??? these contain multiple frequencies, varying in strength over time.?? If we take a snapshot of each frequency present (fundamental frequency and overtones) and their amplitudes, at any one point in time, this snapshot (spectrum) is called a timbre.?? Over time these snapshots will vary.?? For example, if A440 Hz is played on the guitar, and on the piano, we perceive both instruments as playing 440 Hz, but dues to the changing timbre, we perceive one as coming A440 played on a piano, and the other as A440 played on guitar.
Thanks to my granddaughter, Izzy, for adding in the emuso/PracticeSuite PRO interactivity




